精炼几率计算方法是什么？

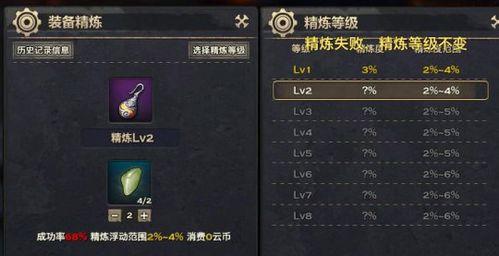
在数据统计、概率分析和风险评估等多个领域中，了解和掌握精炼几率计算方法对于准确预测和制定决策至关重要。精炼几率计算方法究竟有何特别之处？本文将为您提供精炼几率计算的详细步骤，并在过程中引导您通过每个操作环节，帮助您深入理解这一概念。

精炼几率计算方法，通常也被称为后验概率计算或者贝叶斯概率更新方法。在统计学和概率论中，它用于在已知某些其他事件发生的条件下，更新或计算某一事件发生的概率。与传统的先验概率相比，精炼几率的计算方法更加注重于在新信息或证据出现时，概率的动态调整。

二、计算精炼几率所需的关键步骤

1.理解先验概率与条件概率

在开始计算精炼几率之前，您必须熟悉先验概率（事件发生之前的概率）和条件概率（在给定某些信息或条件的情况下，事件发生的概率）的概念。

2.定义可能的假设和证据

假设（H）是指在进行概率计算时，我们对某一事件发生的预期。证据（E）则是指在计算过程中出现的新信息或数据。

3.应用贝叶斯定理

精炼几率计算的核心是贝叶斯定理，其表达式如下：

\[P(H|E)=\frac{P(E|H)\timesP(H)}{P(E)}\]

其中：

\(P(H|E)\)表示在证据E出现的条件下，假设H成立的精炼几率（后验概率）。

\(P(E|H)\)是在假设H成立的条件下，观察到证据E的条件概率。

\(P(H)\)是假设H成立的先验概率。

\(P(E)\)是在所有可能的假设下观察到证据E的概率。

4.收集和分析数据

收集所有与假设和证据相关的数据，并进行分析，以便计算出上述定理中的各个概率值。

5.代入贝叶斯公式计算

将收集到的数据代入贝叶斯公式中进行计算，得到精炼几率（后验概率）。

6.分析结果并制定决策

根据计算得出的精炼几率，对事件做出进一步的分析和预测，并据此制定相关的决策。

三、精炼几率计算中的常见问题

1.如何确定先验概率？

先验概率是根据过往经验或专家意见设定的。在缺乏足够数据的情况下，可能会采用主观判断来确定。

2.条件概率的计算方法是什么？

条件概率的计算涉及分析在特定条件下事件发生的可能性。通常需要依据历史数据或实验结果来计算。

3.如何正确理解并使用贝叶斯定理？

贝叶斯定理允许我们在新的证据出现时，更新我们的概率估计。它强调了证据对于概率估计的影响，从而使得决策更加精准。

4.精炼几率计算的局限性有哪些？

精炼几率计算虽然强大，但它的准确度依赖于先验概率的设定和新证据的收集。不精确或不完整的信息可能导致不准确的后验概率。

四、实用技巧与深度指导

1.贝叶斯定理的实操应用

为了更有效地应用贝叶斯定理，建议多做实际案例分析，这能够帮助您熟练掌握各种概率的计算和应用。

2.利用专业工具辅助计算

现在有很多软件和在线工具可以帮助进行复杂的概率计算。例如使用R语言、Python的SciPy库等，它们都提供了贝叶斯统计的相关功能。

3.理解不同情境下的应用差异

不同的应用场景可能需要不同的处理方式。在医疗诊断中，精炼几率可以帮助医生根据患者的症状和检测结果来更新诊断的准确性。

4.经常回顾和更新先验概率

在现实世界中，情况总是在变化的。定期回顾和更新先验概率，确保其反映最新的信息，对于做出准确的精炼几率计算至关重要。

五、

精炼几率计算是一种强大的统计工具，它通过考虑新的证据来更新我们的概率估计。掌握这种方法能帮助我们在不确定的环境中做出更好的决策。无论是数据分析、风险评估还是科学实验，精炼几率计算都能提供宝贵的信息支持。希望本文的介绍能让您对精炼几率计算有了更深刻的理解，并能在实际问题中应用这一技巧。